MODUL 4
RLC SERI DAN RLC PARALEL
1. Pendahuluan[kembali]
Rangkaian RLC seri adalah suatu tipe rangkaian elektronika yang terdiri dari tiga komponen utama: resistor (R), induktor (L), dan kapasitor (C) yang disusun secara berurutan dalam satu jalur arus yang sama. Dalam rangkaian RLC seri, sinyal arus yang melewati rangkaian harus melalui semua komponen dalam urutan tersebut.
Salah satu aspek penting dari rangkaian RLC seri adalah fenomena resonansi, di mana impedansi total rangkaian menjadi minimum pada frekuensi tertentu. Resonansi terjadi ketika reaktansi induktor (XL) dan reaktansi kapasitor (XC) memiliki nilai yang sama dan saling meniadakan. Pada saat itu, arus yang mengalir dalam rangkaian menjadi maksimum.
Rangkaian RLC paralel adalah jenis rangkaian elektronika di mana resistor (R), induktor (L), dan kapasitor (C) tersusun secara paralel, artinya masing-masing komponen terhubung langsung ke sumber tegangan yang sama.
Rangkaian RLC paralel memiliki frekuensi resonansi di mana impedansi totalnya menjadi minimum. Pada frekuensi resonansi, reaktansi induktor dan reaktansi kapasitor saling meniadakan sehingga hanya resistansi yang berkontribusi terhadap impedansi total.
2. Tujuan [kembali]
1. Dapat mengetahui bagaimana prinsip kerja rangkaian RLC seri dan RLC paralel
2. Dapat membuktikan impedansi (Z) dari sebuah rangkaian RLC seri dan RLC paralel
3. Dapat mempelajari hubungan antara impedansi dengan reaktansi kapasitif, reaktansi induktif, dan sudut fasa pada rangkaian RLC seri dan RLC paralel
4. Dapat membuktikan hubungan antara tegangan (V), tegangan melewati R (VR), dan tegangan melewati C (VC), tegangan melewati L (VL).
3. Alat dan Bahan [kembali]
A. Alat
1. Instrument
Multimeter
2. Module
3. Base Station
4. Jumper
Jumper
B. Bahan
Resistor
Kapasitor
Induktor
Lampu
4. Dasar Teori [kembali]
1. RC Seri
Impedansi dari sebuah rangkaian RC seri dapat dihitung menggunakan rumus
Cara lain untuk menghitung impedansi dengan menggunakan hubungan antara segitiga dan sudutnya. Jika dua sisi segitiga yang dilambangkan dengan R dan XC diketahui sisi ketiga atau Z dapat dicari dengan menggunakan sudut phasa dari R dan Z.
Gambar 4.1. Grafik Hubungan Antara R, XC, dan Z
Impedansi dapat dicari dengan menggunakan harga θ dan rumus:
Dalam rangkaian RC seri arus meninggalkan tegangan sebesar θ, yang disebut sebagai sudut fasa. Sudut fasa θ antara V dan I sama seperti sudut θ antara Z dan R dalam diagram fasor impedansi pada rangkaian RC. Sudut θ juga sama dengan sudut antara V dan VR.
Gambar 4.2. Rangkaian RC Seri
Nilai dari θ tergantung pada nilai XC, R dan Z yang diberikan oleh persamaaan berikut:
Dalam rangkaian RC seri jatuh tegangan melintasi kapasitor (VC), akan tertinggal dari tegangan jatuh pada tegangan resistor (VR). Arus I adalah sama di semua bagian dari rangkaian RC seri seperti gambar 6.2. Arus digunakan sebagai perbandingan fasor yang menunjukkan VR dan Vc dalam gambar 6.3. Fasor VR adalah tegangan yang melewati C.
Gambar 4.3. Hubungan VR, VC, dan V
Dengan rumus Phitagoras didapatkan:
Dari gambar 6.3 juga menunjukkan hubungan antara tegangan V dan arus I dalam rangkaian RC seri. Arus I menunjukkan tegangan V terhadap sudut θ. Dari diagram fasor tegangan didapatkan:
Atau tegangan melewati resistor adalah:
Dari gambar 6.3 juga didapatkan:
Jadi,
Kapasitansi terjadi jika dua buah konduktor dipisahkan oleh sebuah nonkonduktor atau dielektrik. Satuan dari kapasitansi adalah Farad. Kapasitor digunakan dalam banyak hal, di antaranya untuk menyimpan tenaga. Kapasitor dapat menyimpan muatan elektron atau Q untuk beberapa saat.
Hubungan antara muatan Q dari sebuah kapasitor dengan kapasitansi (C) kapasitor ditunjukkan oleh rumus:
Dimana:
Q = muatan (Coulombs)
C = kapasitansi (Farad)
V = tegangan (Volt)
Waktu yang dibutuhkan oleh kapasitor untuk mengisi penuh disebut time constant, dinyatakan dalam rumus:
Dimana:
τ = muatan
(Coulombs) R =
resistansi (Ohm)
C = kapasitansi (Farad)
2. RLC Seri
2.1 Impedansi pada Rangkaian RLC Seri
Gambar 4.4. Rangkaian RLC Seri
Reaktansi pada rangkaian AC tergantung pada frekuensi sumber. Perubahan nilai reaktansi dipengaruhi oleh perubahan frekuensi. Dimana arus dan tegangan yang melintasi reaktansi tidak berada dalam satu fasa. Untuk induktansi murni (R = 0), tegangan mendahului arus yang melalui induktansi sebesar 90 ̊. Untuk kapasitansi murni, arus mendahului tegangan sebesar 90 ̊.
Induktor dan resistor yang terhubung seri pada rangkaian tergantung pada frekuensi dan ukuran dari induktor. Dalam rangkaian RL seri, arus tertinggal dari tegangan sebesar kurang lebih 90 ̊.
Ketika kapasitor terhubung seri dengan resistor, reaktansi dari kapasitor dan resistansi resistor secara bersamaan akan mempengaruhi arus AC. Pengaruh dari kapasitor juga ditentukan oleh ukuran dan frekuensinya. Pada rangkaian RC seri, arus AC mendahului tegangan sebesar kurang lebih 90 ̊. Ini bisa dilihat dari karakteristik induktansi dan kapasitansi yang mempunyai efek berlawanan baik arus maupun tegangan dalam rangkaian AC. Dalam rangkaian, diagram fasor menunjukkan XL lebih besar dari XC.
Impedansi pada rangkaian RLC seri bisa dihitung dengan rumus :
Sedangkan impedansi juga dapat dihitung dengan menggunakan sudut.
2.2 Efek Perubahan Frekuensi dalam Rangkaian RLC Seri
Dalam percobaan ini akan dibuktikan bahwa impedansi Z yang diberikan oleh rumus:
Dimana X adalah selisih antara XL – XC.
Rumus di atas memperlihatkan bahwa jika XL = XC, maka impedansi rangkaian akan mencapai nilai minimum (yaitu dengan harga R). Sedangkan I akan mencapai nilai maksimum. Pada percobaan ini kita akan melihat pengaruh dari perubahan frekuensi apabila di variasikan di sekitar fR.
Pada rangkaian RLC seri yang dilakukan sebelumnya kita telah dapatkan bahwa selama frekuensi dari tegangan sumber dinaikkan pada selang fR, maka XL akan ikut naik sedangkan XC akan turun. Di sisni rangkaian berprilaku seperti sebuah induktasi dimana X akan naik selama f dinaikkan. Dan sewaktu frekuensi di turunkan dari harga fR, XC akan naik sedangkan XL akan turun. Dan disini rangkaian akan berprilaku seperti kapasitansi dengan X akan naik selama frekuensi diturunkan.
2.3 Frekuensi Resonansi RLC Seri
Dalam gambar 6.4, tegangan V dihasilkan dari generator AC yang frekuensi dan
tegangan keluarannya diatur secara manual. Untuk frekuensi dan tegangan V tertentu,
arus akan dihasilkan pada rangkaian yang diberikan oleh persamaan berikut:
Dimana Z adalah impedansi pada rangkaian.
Tegangan jatuh melintasi R, L dan C akan diberikan oleh IR, IXL, dan IXC. Jika frekuensi generator diubah dengan V tetap, arus dan tegangan jatuh melintasi R, L dan C akan berubah. Frekuensi ini adalah fR, yang lebih dikenal dengan frekuensi resonansi, dimana:
Frekuensi resonansi bisa dihitung dengan rumus:
Dan
Ketika XL = XC, maka f = fR.
Jadi,
Sehingga didapatkan,
Karakteristik dari rangkaian resonansi seri adalah:
1. Tegangan jatuh melintasi komponen reaktif adalah sama dengan hasil perkalian antara arus I dalam rangkaian dengan reaktansi X dari komponen.
2. Pengaruh reaktif total dari sebuah rangkaian adalah selisih antara reaktansi kapasitif XC dengan reaktansi induktif XL.XC dengan reaktansi induktif XL.
3. Impedansi Z dari rangkaian RLC seri adalah:
4. Impedansi Z dari rangkaian adalah minimum ketika XL = XC, dan pada saat ini arusI adalah maksimum.
3. RLC Paralel
3.1 Impedansi pada Rangkaian RLC Paralel
Gambar 4.5. Rangkaian RLC Paralel
Pada rangkaian RLC paralel, masing masing R, L dan C mempunyai tegangan yang sama, V. Sedang arus yang lewat R adalah IR, L adalah IL dan C adalah Ic. Perhitungan untuk besar arus pada masing masing beban :
Jalannya fase arus dan tegangan serta diagram fasornya seperti berikut :
Gambar 4.6 Diagram Fasor RLC
Fase IR akan dengan V, fase IC akan mendahului fasa V sebesar 90o
sedangfase IL akan ketinggalan 90o dari fase V.
I adalah resultan dari IR, IL dan IC yang dapat dihitung dengan rumus :
Karena V adalah sama, maka diagram fasor bisa juga dinyatakan untuk impedansi sebagai berikut :
Pada frekuensi rendah, nilai impedansi kecil dan arus besar. Ketika frekuensi bertambah impedansi akan bertambah sedang arus akan mengecil. Tepat pada frekuensi resonansi, impedansi akan maksimum (sebesar R) dan arus akan minimum ( sebesar Vt / R). Ketika frekuensi naik lagi, impedansi akan menurun lagi sedang arus akan membesar lagi.
Fase juga akan berubah dari mendekati -90o pada frekuensi rendah, kemudian akan mengecil mendekati 0o .Tepat pada frekeunsi resonansi, besar fase adalah 0o. Fase kemudian akan naik ke mendekati 90o ketika frekuensi naik lagi.















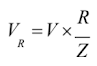














Komentar
Posting Komentar